Kortste pad(en)

Een kortste pad van hier naar daar: dat probleem moet regelmatig opgelost worden, en liefst efficiënt. In deze les/activiteit exploreren de leerlingen verschillende manieren om een kortste pad te vinden op een systematische manier, t.t.z. ze maken een aantal algoritmes die door een computer kunnen uitgevoerd worden en ze bestuderen de eigenschappen van die algoritmes. De leerlingen worden ook uitgedaagd om niet zo voor de hand liggende toepassingen van het kortste-pad-probleem te bedenken.

Een navigatiesysteem - dikwijls gewoon een GPS genoemd - gebruikt een goed kortste-pad-algoritme: je geeft je bestemming in en je krijgt de kortste weg van je huidige positie naar je bestemming. Dikwijls betekent "kortste" dat dit de weg is met een minimaal aantal kilometers. Afhankelijk van de instellingen of voorkeuren, kan "kortste" betekenen dat de voorgestelde weg het minste tijd vraagt, of het minste kost aan tolgeld, en daarmee zijn de mogelijkheden niet op.

Voor toeristen is een GPS plezant, en voor vervoermaatschappijen van groot economisch belang. Ook moeten lange routes snel herberekend kunnen worden als de omstandigheden veranderen: files, kapotte brug, ... Goeie redenen om een efficiënt kortste-pad-algoritme te bestuderen, en om na te denken over in welke omstandigheden zulk algoritme van pas komt.

---

Links met leerplan

• informaticawetenschappen
• probleemoplossend denken

Vaardigheden

• de abstractie van het kortste-pad-probleem begrijpen
• een systematische methode (algoritme) beschrijven
• redeneren over een algoritme i.v.m. de efficiëntie, eindigheid en correctheid

Leeftijd

• 15 jaar en ouder
• in aangepaste vorm ook voor jonger dan 15

Duur

Ongeveer twee lesuren.

Materiaal

• afbeeldingen van gewogen grafen
• potlood, gom en papier
• eventueel ook speelplaats en krijt: zie hier

Verloop

Het verloop van de lesactiviteit is als volgt:

• Fase 1: een klassikale brainstorm over het kortste-pad-probleem
• Fase 2: leerlingen bedenken oplossingsmethoden (algoritmen) voor het kortste-pad-probleem
• Fase 3: het korste-pad-algoritme van Dijkstra wordt aangebracht, geïllustreerd en ingeoefend.

Een nabespreking gaat dieper in op een aantal eigenschappen van de algoritmes, in het bijzonder de efficiëntie van het korste-pad-algoritme van Dijkstra en zijn correctheid.

Fase 1: over het kortste-pad-probleem

Hou een klassikale brainstorm:

• Zoek problemen die op een kortste-pad-probleem gelijken.
• Wat is gemeenschappelijk aan die problemen, wat is de essentie ervan?
• Kan je met een tekening uitdrukken wat gemeenschappelijk is aan al die problemen?

Hints voor leerkracht en leerling

• voorbeelden van kortste-pad-problemen
  • een woordspelletje: transformeer een woord (bv. POES) in een ander woord (bv. HOND) door telkens 1 letter te veranderen en doe dat in zo weinig mogelijk tussenstappen; POES-PONS-POND-HOND geeft een oplossing en je kan inzien dat er geen kortere bestaat; probeer het eens voor de woorden DRA en OLM ... eens je een oplossing hebt: hoe weet je of die oplossing de kortste is?
  • een landkaart van Vlaanderen, met daarop steden, wegen tussen die steden en de lengte van elk stuk weg: zoek de kortste weg tussen bv. Kaulille en Tervate ...
  • i.p.v. de kortste af te leggen afstand, heb je misschien liever de snelste weg; kortste kan dus vanalles betekenen: tijd, afstand, geld (als je tol moet betalen); er is steeds een kost gemoeid met van één punt naar een ander te gaan; van de deeltrajecten worden de kosten opgeteld; de totale kost wil je zo klein mogelijk houden: dat gebeurt langs een kortste pad
  • meer voorbeelden van kost: slijtage, hoogteverschil, brandstofverbruik, lengte file, aantal verkeersdrempels, storm (voor vliegtuig of schip), wegenvignet per land ... kost kan ook samengesteld zijn uit verschillende factoren, bv. kost = 2*tol + 17*km ; kost kan ook emotioneel zijn en niet uit te drukken in een gangbare eenheid, zolang je de kost maar als een positief getal kan uitdrukken
• overeenkomsten aan die problemen:
  • een aantal elementen: hierboven waren dat woorden, of steden; wat die elementen juist zijn is niet belangrijk, wel dat je ze kan benoemen
  • een positief getal dat de kost weergeeft om van een element in één stap naar een ander te gaan als dat mogelijk is; zo kan je van ZEBRA niet in één stap naar PAARD; maar wel van PAPIER naar RAPIER
  • de kost om van één element naar een ander te gaan met toegelaten tussenstappen, is de som van de tussenstappen
  De essentie van al die kortste-pad-problemen wordt gevat in de notie van gewogen graaf : een verzameling punten, en tussen sommige punten een boog met daarop de kost om van het ene punt naar het andere te gaan; het is mogelijk dat de kost om heen te gaan verschilt van de kost om terug te keren; daarom kan bij sommige bogen een pijl staan om de richting aan te geven; parallelle verbindingen tussen twee punten zijn mogelijk (van Leuven naar Brussel kan je langs de E40 of langs de N2), en als er geen boog tussen twee punten is, dan kan je niet rechtstreeks van het ene naar het andere: je hebt tussenstappen nodig. Hieronder zie je een gewogen graaf; de kost van het pad A-B-D is 1+5=6; een korter pad van A naar D is A-C-D met kost 3

  

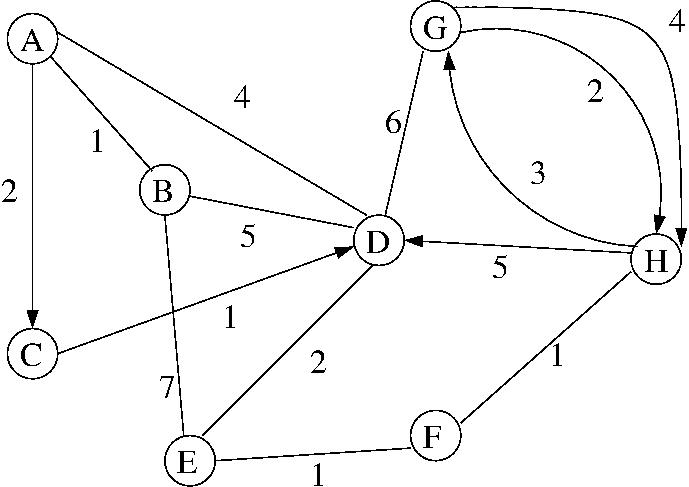
  in grafentheorie is het gebruikelijk de punten knopen of toppen te noemen; de kost wordt gewicht van de boog genoemd - vandaar de naam gewogen graaf ; we spreken ook over de (totale) kost van een pad, of zijn gewicht, of lengte.

Opdracht: teken (een stukje van) de gewogen graaf voor het probleem om het woord DRA om te zetten naar OLM; zie hier voor een mogelijke oplossing; je ziet dat er meer dan één pad van lengte 4 is en misschien is er geen korter; om dat zeker te weten moeten we eigenlijk alle woorden van 3 letters opnemen in de graaf, bogen trekken (met gewicht 1) tussen woorden waartussen de overgang mogelijk is, en dan het kortste-pad-probleem voor die graaf oplossen

Fase 2: het kortste-pad-probleem oplossen

Vertrek van een gewogen graaf - bijvoorbeeld één van de grafen hierboven, of maak er eentje met wat steden en verbindingswegen op: geef ook de afstanden die erbij horen.

Laat de leerlingen individueel of in kleine groepjes op die graaf een kortste pad zoeken tussen twee gegeven knopen. Laat ze vervolgens mondeling rapporteren hoe ze dat kortste pad vonden, t.t.z. welke methode hebben ze gebruikt. Besteed daarbij aandacht aan de volgende vragen:

• Is die methode beschreven zodanig dat iemand anders die methode kan gebruiken of uitvoeren? Laat bijvoorbeeld een groepje leerlingen een methode van een ander groepje toepassen op de graaf, en bespreek in hoeverre dat werkt.
• Werkt die methode altijd? D.w.z. dat die methode een kortste pad geeft voor elke gewogen graaf (en start- en eindpunt). Hierna komt een voor de hand liggende en gemakkelijk te beschrijven methode (dichtste buur) die spijtig genoeg niet altijd werkt.
• Is het een efficiënte methode? Het aantal elementaire stappen tijdens de uitvoering van een kortste-pad-algoritme hangt af van de grootte van de graaf, het aantal knopen. Ook hier komen we op terug in de nabespreking.

Hints voor leerkracht en leerling

• Er zijn minstens twee naieve methodes
  • dichtste buur: vanuit een punt ga je naar het dichtsbijzijnde punt

    wat als twee (of meer) punten even dichtbij liggen en alle andere verder weg? let op dat je niet terugkeert of in een kring loopt; gebeurt het dat je je doel niet bereikt? misschien kan je terugkeren en ergens opnieuw proberen: hoe beschrijf je dat? soms krijg niet echt het kortste pad! bedenk zelf grafen waarbij dat geïllustreerd wordt; of bekijk een aantal voorbeeldgrafen

    de methode is niet perfect, maar het is toch goed om een volledige beschrijving van de methode te laten maken, zodat het concept algoritme ingeoefend wordt: een preciese beschrijving van wat gedaan moet worden die geen ruimte laat voor interpretatie; daarom vragen we dat een andere leerling die methode uitvoert op een gegeven graaf: dubbelzinnigheden, onderspecificatie of tegenstrijdigheden (en fouten) komen dan aan het licht

  • alles proberen:

    stel je moet van A naar Z en de andere punten in de graaf heten B, C en D; dan kan je een lijstje maken met alle potentiéle paden van A naar Z als volgt:

    • geen tussenliggend punt: A-Z
    • een tussenliggend punt: A-B-Z, A-C-Z, A-D-Z
    • twee tussenliggende punten: A-B-C-Z, A-B-D-Z, A-C-B-Z, A-C-D-Z, A-D-B-Z, A-D-C-Z
    • drie tussenliggende punten: A-B-C-D-Z, A-B-D-C-Z, A-C-B-D-Z, A-C-D-B-Z, A-D-B-C-Z, A-D-C-B-Z

    sommige paden zijn onmogelijk omdat er geen verbinding is; van de andere maak je de som van de gewichten en je houdt een kleinste als resultaat

Conclusie: dichtste buur gaat snel, maar werkt niet altijd; alles proberen werkt altijd, maar vraagt veel werk en is traag. Deze beschrijving van de dichtste-buur methode kan je gebruiken op een aantal grafen: wat kan je nog precieser formuleren?

Mogelijke uitbreiding: tel hoeveel potentiele paden het alles proberen algoritme uitprobeert en zet dat in een grafiek met op de x-as het aantal punten in de graaf: neem dat aantal niet te hoog!

Merk op: het zoeken/vinden van een kortste pad is niet hetzelfde als het doorlopen van een kortste pad: in het eerste geval leg je misschien heel wat meer afstand af, maar dat is op papier, het is tijdens de uitvoering van het algoritme; je begint pas aan je echte reis nadat het algoritme een kortste pad heeft gevonden

Ondertussen heb je door: we spreken wel over het kortste pad, maar dikwijls is er meer dan één kortste pad, t.t.z. verschillende paden met dezelfde minimale kost.

Fase 3: het algoritme van Dijkstra

E. W. Dijkstra ontwierp een zeer efficiënt algoritme om een kortste pad te vinden. Het heeft de voordelen t.o.v. de vroeger geziene algoritmen dat het altijd werkt, gegarandeerd een kortste pad vindt (als een pad bestaat) en geen overbodig werk doet.
Het algoritme van Dijkstra houdt bij elk punt in de graaf een label bij; stel we zoeken een kortste pad van A naar Z; een label bij een knoop X bevat drie items:

• het vorige punt in het voorlopig kortste pad van A naar X; we noteren dit als voorganger(X)
• de afstand van het voorlopig kortste pad van A naar X; we noteren dit als kortste_afstand(X)
• een aanduiding of het punt X te wachten staat om op de todo lijst gezet te worden wacht , ofwel op de todo lijst staat tedoen , ofwel helemaal klaar is klaar ; we noteren dat als status(X)

De kost om van X naar Y te gaan zullen we aanduiden met kost(X,Y) : alternatief denk je aan de lengte van de boog of het gewicht.

Het algoritme bestaat uit twee delen: een initialisatie en een lus. Er hoort telkens een demo bij die dat stukje algoritme uitvoert op een voorbeeld.

Initialisatie

De initialisatie van het algoritme zorgt dat de labels de juiste waarde krijgen in het begin: je kan je inbeelden dat die labels stukjes papier zijn waarop een en ander geschreven staat. Indien de graaf getekend is op de speelplaats, dan liggen die papiertjes bij de punten van de graaf. In het begin van het algoritme weten we van het label van de beginknoop A, dat er geen vorige knoop in het pad is, dat de afstand van A naar A gelijk is aan nul, en dat A op de todo lijst staat. Van de andere knopen weet je nog niks en die staan te wachten. Hieronder de beginsituatie voor een graaf met vier knopen A, B, C, Z en wat bogen ertussen.

Demo: de initialisatie

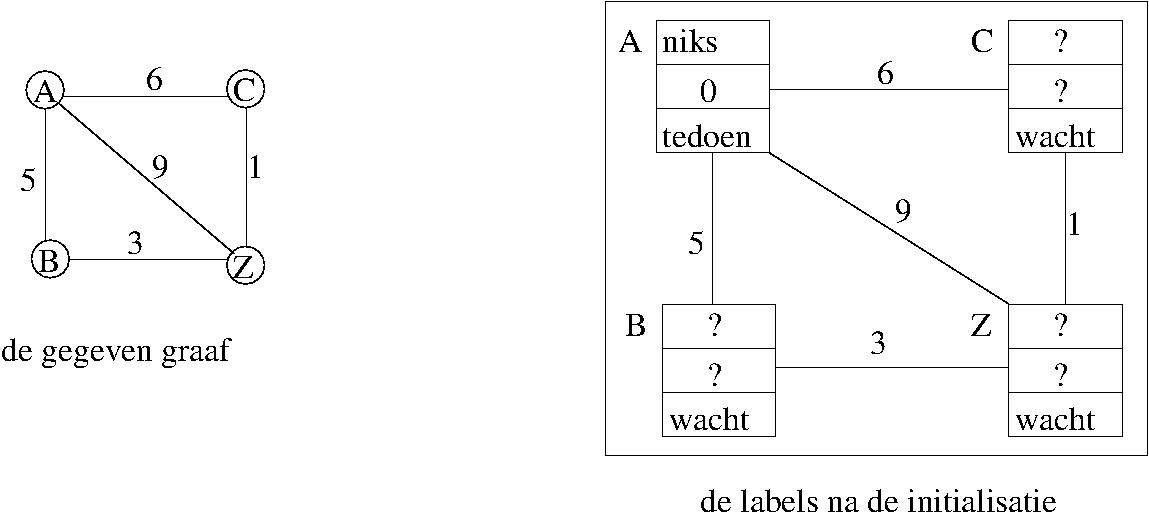
Na de initialisatie gaat het algoritme als volgt:

Vervolg van het algoritme: de lus

herhaal:

1. kies een tedoen-knoop X met kleinste kortste_afstand(X); indien de gekozen knoop gelijk is aan Z, stop : na het uitgewerkte voorbeeld staat hoe de labels een kortste pad opleveren; indien er geen tedoen-knoop meer bestaat, stop want er is geen pad van A naar Z
2. pas het label van de buren Y van X aan; dit wil zeggen
   
   voor elke buur Y van X doe:
   • indien Y klaar is, laat het label zoals het was, anders
   • indien Y wacht,
     • schrijf dan in zijn label dat het pad van X komt

       (t.t.z. voorganger(Y) ← X)

     • tel de afstand op de boog bij de afstand tot X en vul in in het label van Y

       (t.t.z. kortste_afstand(Y) ← kortste_afstand(X) + kost(X,Y))

     • en zet Y op tedoen

       (t.t.z. status(Y) ← tedoen),

     anders
   • Y heeft een tedoen label en misschien kan het pad tot Y korter worden:
     • indien (kortste_afstand(X) + kost(X,Y) ≥ kortste_afstand(Y)), laat het label zoals het was;
     • anders

       voorganger(Y) ← X
       kortste_afstand(Y) ← kortste_afstand(X) + kost(X,Y)

3. zet X op klaar
   (tt.z. status(X) ← klaar)

Demo: de lus

Hieronder staan de labels in het voorbeeld telkens nadat een nieuwe knoop op klaar kwam te staan:

nadat A klaar is:

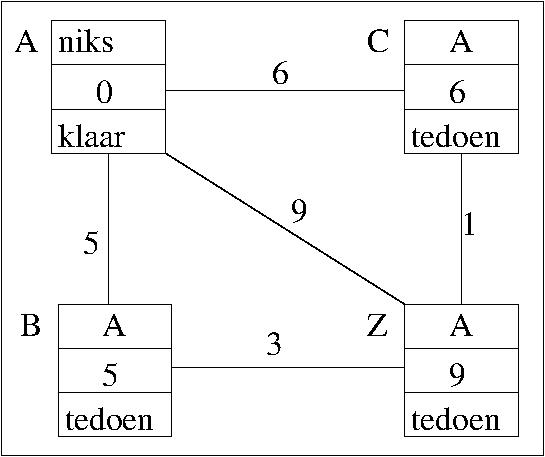
nadat B klaar is

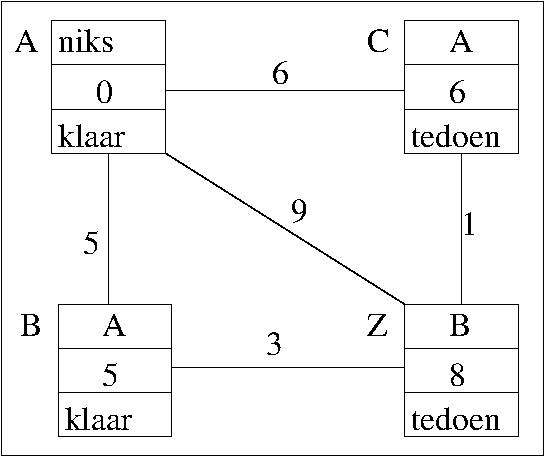
Merk op dat Z nu al een voorlopig kortste afstand heeft maar dat die nog verbeterbaar is

nadat C klaar is

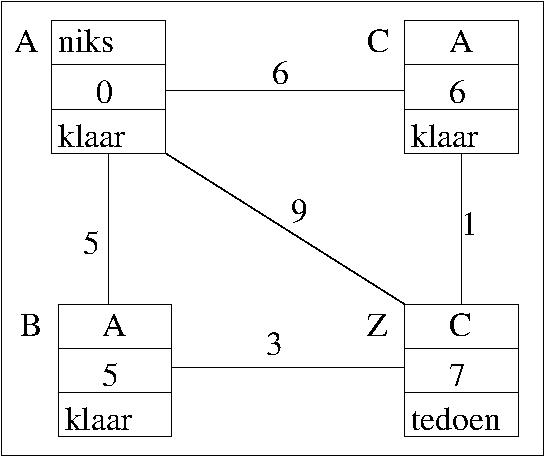
nu is Z het tedoen-punt met de kleinste kortste_afstand en wordt gekozen in punt 1 van het algoritme: het algoritme stopt

Om het algoritme af te sluiten: Bij stop heeft het algoritme genoeg informatie verzameld om het (omgekeerde) kortste pad te construeren: vertrek vanaf Z en ga "achterwaarts", t.t.z. naar het punt in het voorganger-veld van het label. Doe dat tot je bij A komt. De lengte (of kost) van het kortste pad staat in het label als kortste_afstand(Z).

In het voorbeeld gebeurt dat als volgt: het omgekeerde kortste pad begint bij Z; voorganger(Z) is C, dus nu hebben we al het pad Z-C; voorganger(C) is A, dus hebben we als pad Z-C-A; voorganger(A) is niks, dus het pad is af; de lengte van het kortste pad vind je in het label van Z als kortste_afstand(Z) .

Inoefenen

Probeer op de voorbeeldgrafen zowel het dichtste-buur-algoritme en Dijkstra uit, of op grafen die je zelf ontwerpt, of misschien op een kaart van Vlaanderen.

Nabespreking

Hier zijn een aantal mogelijke onderwerpen voor een nabespreking:

Hoeveel werk moet het algoritme doen? Stel er zijn N punten in de graaf, dan kunnen we een bovengrens berekenen voor het aantal elementaire operaties die uitgevoerd worden

• in punt 1 van het algoritme moet van de tedoen labels een label met kleinste kortste_afstand gezocht worden; zonder speciale inspanning kost dat elke keer hoogstens N operaties [bekendheid met lineair zoeken helpt, maar het kan een gelegenheid zijn om dit aan te brengen]; dat kan niet meer dan N keer nodig zijn; dus punt 1 doet ongeveer N*N werk
• van elk punt X kan het label 1x overgaan van tedoen naar klaar; op dat ogenblik moeten de buren van X overlopen worden; X heeft hoogstens N-1 buren; dat betekent hoogstens N*(N-1) aanpassingen

We komen uit op a*N*N operaties waarbij die a een constante is, onafhankelijk van de grootte van de graaf. We zeggen: het algoritme is kwadratisch in het aantal punten. Voor een graaf met twee keer zoveel punten heeft het algoritme vier keer zoveel tijd nodig.

Wat als er in punt 1 van het algoritme twee tedoen-punten zijn met dezelfde kleinste kortste_afstand? Maakt het uit welk punt het algoritme (eerst) kiest? Hangt de lengte van het kortste pad ervan af, of het pad? Bedenk grafen om te illustreren wat je hier antwoordt.

Voor welke grafen komt het algoritme in de tweede stop van punt 1 van het algoritme van Dijkstra?

Bestaat er altijd een kortste pad? Als er geen enkel pad van A naar Z bestaat, dan bestaat er zeker geen kortste pad. Kan je hard maken dat indien er minstens één pad bestaat, er ook een kortste pad bestaat? Pas op, want een verzameling zoals {1/n|n in de natuurlijke getallen} heeft geen kleinste element.

Dijkstra is correct

Het redeneren over en het bewijzen van de correctheid van een algoritme is subtiel en verschilt van bewijzen in de wiskunde: een algoritme is een dynamisch proces, en het verandert dingen - bijvoorbeeld de items in de labels van het algoritme van Dijkstra. In het algemeen proberen we van één of meerdere uitspraken aan te tonen dat die waar zijn op een bepaalde plaats in het algoritme, en dat bij het stoppen van het algoritme, die uitspraken impliceren wat we willen dat het algoritme doet. Zulke uitspraken worden invarianten genoemd, omdat ze dikwijls invariant zijn voor het doorlopen van een lus. Invariant betekent dan "telkens waar als de lus doorlopen wordt". Meer concreet voor Dijkstra:

1. als status(X) == klaar of tedoen, dan heeft het pad van A naar X (achterwaarts geconstrueerd vanaf X door voorganger te volgen) een lengte gelijk aan kortste_pad(X)
2. als status(X) == klaar, dan is kortste_pad(X) de lengte van een kortste pad van A naar X

Beide uitspraken zijn waar na de initialisatie, en dus ook de eerste keer dat de lus binnengegaan wordt. Het komt er nu op aan om aan te tonen dat als de uitspraken waar zijn bij het binnenkomen van de lus, ze nog waar zijn nadat de lus één keer is uitgevoerd. Dit kan verder uitgewerkt worden, informeel of formeel, al naargelang.

Variatie

Als gewerkt wordt met grafen die uitgetekend zijn op de speelplaats, dan kan je papiertjes met de labels bij elk punt leggen. Het aanpassen van de labels van de buren van een punt in 2 van het algoritme kan in parallel : verschillende leerlingen kunnen tegelijkertijd een andere buur behandelen. Hoeveel leerlingen heb je nodig om zoveel mogelijk in parallel te doen? Hoe verhinder je dat twee leerlingen tegelijkertijd het label van een punt proberen aan te passen?

Nog meer weten over algoritmen?

Al wat ouder, maar eeuwig relevant ... sneeuwvlokjes en informatica toont het verband tussen wat je kan tekenen (met een computerprogramma) en wat je kan berekenen: de gemeenschappelijke begrenzingen worden in de verf gezet.

Geïnteresseerd in opleiding/nascholing?

Progra-MEER richt workshops in die passen in de nascholingsprogrammas van verschillende universiteiten. En de vakvereniging voor leerkrachten informatica 2link2 kondigt ook andere initiatieven aan.